介绍
由于基于反向传播的参数梯度的计算无法用在不可微的层上,导致具有离散变量的随机网络很难训练。之前的关于随机梯度估计的工作主要集中在:
- 用蒙特卡洛方差约减技术扩充的得分函数估计
- 用于Bernoulli变量的有偏路径导数估计(biased path derivative estimator)
然而,还没有专门针对类别变量(Categorical Variable)的梯度估计方法。Gumbel Softmax的引入解决了这一问题,它是单纯形(simplex)上的一个连续分布,可以近似类别样本,它的参数梯度可以很容易地通过重参数化(Reparameterization)技巧计算出来。实验表明,Gumbel-Softmax在伯努利变量和类别变量上都优于所有单样本梯度估计。
Gumbel-Softmax Distribution
本节定义Gumbel-Softmax分布,它是一个单纯形上的一个连续分布,可以用来近似来自类别分布(categorical distribution)的样本。令$z$为一个类别变量,每个类别的概率为$\pi_1,\pi_2,\cdots\pi_k$。假设类别样本被编码为位于$(k-1)$维单纯形$\Delta^{k-1}$的“corner”上的$k$维one-hot向量。
Gumbel-Max trick提供了一个简单高效的方式来从一个类别分布中以类别概率$\pi$抽取样本$z$:
\(z = one\_hot(argmax_i[g_i+log\pi_i]) \tag{1}\)
其中$g_1\cdots g_k$是从Gumbel(0, 1)分布中抽取的独立同分布样本。对Gumbel(0, 1)分布采样可以使用逆变换采样,通过从均匀分布$u\sim \rm{Uniform(0, 1)}$中抽取$u$,然后计算$g=-log(-log(u))$得到。
这里可能会有疑问:为什么不直接从类别分布中采样呢?为解答这个问题,需要介绍来自VAE中的reparameterization trick。通过从一个固定的分布中采样$g$并使用$\pi$来重参数化这个分布,避免了必须反向传播通过随机节点(在这里指采样得到的$g$)。取而代之的是只需要反向传播到确定性的重参数化,更新概率$\pi_i$。
我们使用softmax函数来作为argmax的一个连续、可微的近似,并且生成$k$维的样本向量$y\in\Delta^{k-1}$,其中:
\(y_i=\frac{exp(log(\pi_i)+g_i)}{\sum_{j=1}^{k}exp((log(\pi_j)+g_j)/\tau)},\;for\; i=1,\cdots,k. \tag{2}\)
Gumbel-Softmax分布的概率密度函数为:
\(p_{\pi,\tau}(y_1,\cdots,y_k)=\Gamma(k)\tau^{k-1}(\sum_{i=1}^k\pi_i/y_i^\tau)^{-k}\prod_{i=1}^k(\pi_i/y_i^{\tau+1}) \tag{3}\)
temperature参数$\tau$越接近0,从Gumbel-Softmax分布采样得到的样本就越接近于one-hot向量,Gumbel-Softmax分布也就越接近于类别分布(categorical distribution)。相反地,$\tau$越大,得到的分布越接近于(对各类别的)均匀分布。
Reparameterization trick
以VAE举例,如下图:
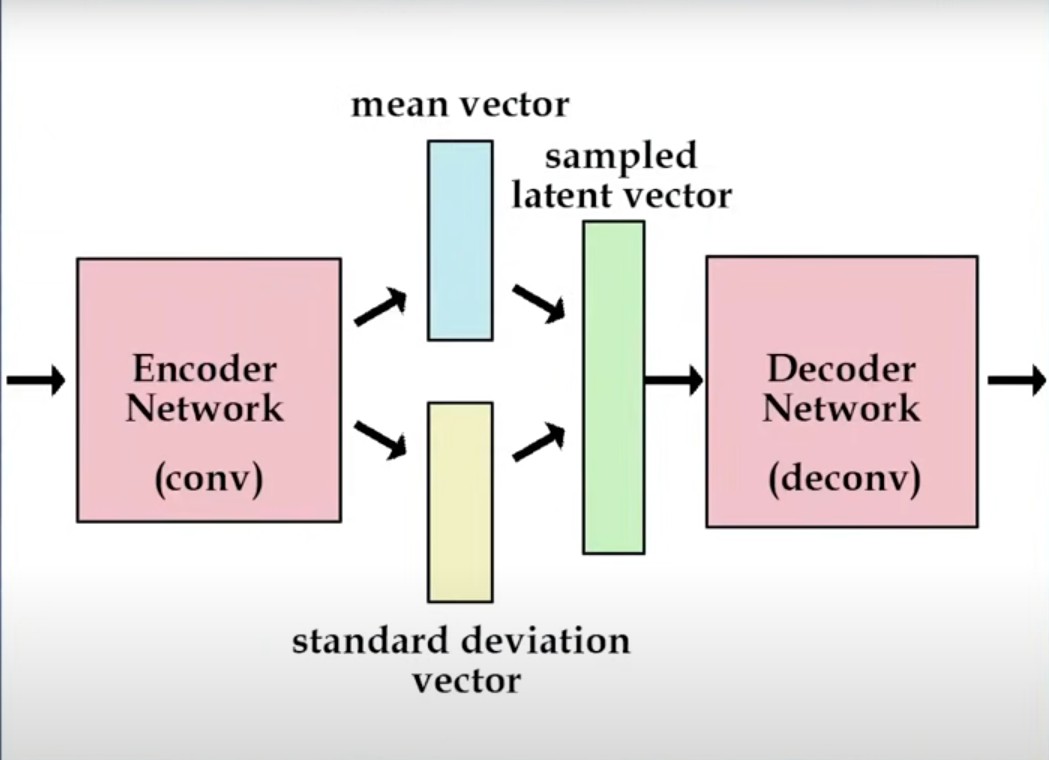 图中有一个采样操作(对应计算图中的sampling node),而无法通过sampling node做梯度的反向传播。Reparameterization trick就是为了解决这一问题,它将latent vector $z$看做:
\(z=\mu+\sigma\odot\epsilon,\;where\;\epsilon\sim Normal(0, 1) \tag{4}\)
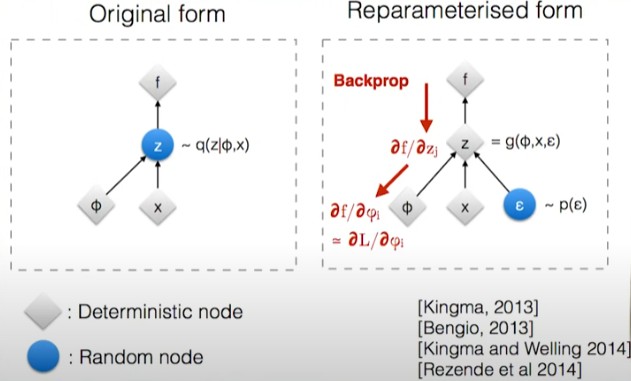
图中有一个采样操作(对应计算图中的sampling node),而无法通过sampling node做梯度的反向传播。Reparameterization trick就是为了解决这一问题,它将latent vector $z$看做:
\(z=\mu+\sigma\odot\epsilon,\;where\;\epsilon\sim Normal(0, 1) \tag{4}\)
其中$\mu$和$\sigma$是要学习的参数,$\epsilon$是引入的随机部分,它服从标准正态分布。通过这一步,可以使梯度顺畅地反向传播到要学习的参数$\mu$和$\sigma$,而$\epsilon$对应的是一个固定的stochastic node,我们不需要对它求导也不会改变它的参数,所以无所谓该node是否做sampling操作。如下图所示:
Gumbel-Softmax Estimator
Gumbel-Softmax分布对于$\tau>0$是光滑的,所以可以计算关于参数$\pi$的导数$\partial y/\partial\pi$。因此,通过将类别样本替换为Gumbel-Softmax样本,我们便可以使用反向传播来计算(近似)梯度。在训练过程中用可微的近似来代替不可微的类别样本的过程叫做Gumbel-Softmax estimator。
尽管Gumbel-Softmax样本是可微的,对于非零的temperature,它和对应的类别分布仍不是完全相等的。关于训练,存在一个tradeoff:
- 对于小的temperature,样本接近于one-hot,但梯度的方差很大
- 对于大的temperature,样本是平滑的,但梯度的方差很小(不同的category区分力度小)
在作者的实验中,发现temperature参数$\tau$可以按照不同的schedule做退火并保持不错的性能。如果$\tau$是一个可学习的参数(相对于通过固定的schedule进行退火),这一(退火)机制可以被看做熵正则(entropy regularization),此时Gumbel-Softmax分布可以在训练过程中自适应地调节给出样本的可信度。
Straight-Through Gumbel Estimator
对于被限制在离散值采样的场景(比如强化学习中从离散的动作空间采样,或者量化压缩),我们在前向推理中使用argmax离散化$y$,但在反向传播过程中仍使用soft版本的y,通过$\nabla_\theta z\approx\nabla_\theta y$来近似真实梯度。这一过程叫做Straight-Through(ST)Gumbel Estimator,它允许在$\tau=0$的情况下仍然可以做梯度估计。ST Gumbel Softmax与偏路径导数估计有相似之处,它允许即使在$\tau$很高的情况下,样本也是稀疏的。
为了保证采样输出$y_{hard}$是严格one-hot并且这一过程是可微的,而反向传播的梯度等于$y_{soft}$输出的梯度。需要使用一个trick:$y_{hard}$-stop gradient($y_{soft}$)+$y_{soft}$,这通过剔除所有其它梯度来使得梯度值等于$y_{soft}$的梯度。
Gumbel-Softmax的缺点
- $\tau\gt0$时,GS分布与真正的类别分布并不完全相同。这意味着这个过程相比于真实(categorical distribution的)梯度是一个有偏估计(biased estimator)
- 对于很小的$\tau$,GS分布的梯度方差很大,这不利于stochastic神经网络的训练。因此,需要在variance和bias之间做出权衡
- $\tau\gt0$时,样本不是离散的,因此我们并不是真的在执行hard动作,而是近似这一过程(只是相比于softmax更加“陡峭”)。
代码
TensorFlow
import tensorflow as tf
def sample_gumbel_01(shape, eps=1e-10):
"""Sample from Gumbel(0, 1) distribution"""
U = tf.random.uniform(shape, minval=0, maxval=1, dtype=tf.float32)
return -tf.math.log(-tf.math.log(U + eps) + eps)
def gumbel_softmax_sample(logits, temperature):
"""Draw a sample from the Gumbel-Softmax distribution"""
# logits: [batch_size, n_classes], unnormalized log-probs
y = logits + self.sample_gumbel_01(tf.shape(logits))
return tf.nn.softmax(y / temperature, axis=-1) # sum of each line equals 1
def gumbel_softmax(logits, temperature, hard=False):
"""
logits: [batch_size, n_classes], unnormalized log-probs
temperature: non-negative scalar
hard: if True, take argmax, but differentiate w.r.t. soft sample y
"""
y = gumbel_softmax_sample(logits, temperature)
if hard:
y_hard = tf.one_hot(tf.math.argmax(y, axis=-1), depth=y.shape[1], dtype=y.dtype)
# ref: https://pytorch.org/docs/stable/generated/torch.nn.functional.gumbel_softmax.html#torch.nn.functional.gumbel_softmax
# https://gist.github.com/yzh119/fd2146d2aeb329d067568a493b20172f?permalink_comment_id=3037101#gistcomment-3037101
# use stop_gradient trick to forward the gradient w.r.t. y_hard to y
return tf.stop_gradient(y_hard - y) + y
else:
return y
# Or using tf_agents
# https://www.tensorflow.org/agents/api_docs/python/tf_agents/distributions/gumbel_softmax/GumbelSoftmax
import tf_agents
tf_agents.distributions.gumbel_softmax.GumbelSoftmax(
temperature,
logits=None,
probs=None,
dtype=tf.int32,
validate_args=False,
allow_nan_stats=True,
name="GumbelSoftmax"
)
# Or using tensorflow_probability
# https://www.tensorflow.org/probability/api_docs/python/tfp/distributions/RelaxedOneHotCategorical
import tensorflow_probability as tfp
tfp.distributions.RelaxedOneHotCategorical(
temperature,
logits=None,
probs=None,
validate_args=False,
allow_nan_stats=True,
name='RelaxedOneHotCategorical'
)
Reference
[1] Categorical Reparameterization with Gumbel-Softmax
[2] A Review of the Gumbel-max Trick and its Extensions for Discrete Stochasticity in Machine Learning
[3] Blog: Gumbel Softmax
[4] Variational Autoencoders