为什么是Transformer
我们知道,RNN模型的训练中会有梯度消失/爆炸的问题,这是因为同样的参数会在不同的时间步重复使用,造成RNN的error surface变化特别剧烈(有些区域非常“平坦”,即梯度很小,有些地方却非常“陡峭”,即梯度很大)。LSTM的提出一定程度上解决了梯度消失的问题:RNN通过memory cell,信息可以被加权后以相加的方式“保存”起来,除非用forget gate将其擦除。这样可以移除error surface中特别“平坦”的区域,从而解决梯度消失的问题。【注】LSTM仍无法解决梯度爆炸的问题(因此,训练LSTM需要将学习率设小一些)。
传统的序列模型对于序列很长的情况,很难避免“遗忘”的问题。这一“遗忘”是由梯度随时间反向传播(Back propagation through time)造成的,序列中越“久远”的元素,其梯度贡献占比越少。且序列越长,遗忘现象越严重。
2015年ICLR上attention的提出可以用来避免“遗忘”问题,随之的代价是算法复杂度的上升。Transformer是attention的集大成者,其完全抛弃了RNN,单纯使用attention来做序列处理并达到了远超传统序列模型的SOTA。笔者认为,可以将attention看做是改良版的memory cell,以一种更直接的方式来保存历史信息。
Transformer模型介绍
Transforme于2017年NIPS的Attention Is All You Need提出。Transformer是Encoder和Decoder两部分组成的Seq2Seq模型,仅由attention和全连接层组成。由于没有RNN结构,使得算法实现更容易并行,从而实现更高的计算效率。
1. Positional Encoding
Transformer舍弃了RNN中的recurrence机制以支持multi-head self-attention机制,这使得训练过程得到大幅加速。然而,由于序列中的每个word同时进入模型(Encoder和Decoder),模型无法分辨序列中word的位置信息。位置信息是有用的,比如对于因果、前后顺序等场景。为此,需要人为加入位置信息。Transformer中采用了positional encoding这一方法,这一方法的好处在于:(1)可以适应测试数据比训练数据还长的场景,即位置信息编码不受限于具体场景,且不要求训练数据覆盖任何句子长度;(2)可以反映出相对位置的一致性,即间隔特定word数的词段哪怕从句首换到句尾,它们之间的相对位置是不变的;(3)值的取值范围是有界的;(4)每个位置的值是确定性的。
作者使用了不同频率的sine和cosine函数来实现位置编码:
\(PE_{pos,2i}=sin(pos/10000^{2i/d_{model}}) \\
PE_{pos,2i+1}=sin(pos/10000^{2i/d_{model}}) \tag{1}\)
上式中$d_{model}=512$为输入embedding的维度。$i$的取值范围是$[0,\cdots,d_{model}/2)$,对每个位置,都会生成一个$d_{model}$维的postional encoding。官方代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
import tensorflow as tf
# get radian by broadcasting
def get_angles(pos, i, d_model):
# pos: (position, 1), angle_rates: (1, d_model)
angle_rates = 1 / np.power(10000, (2 * (i // 2)) / np.float32(d_model))
return pos * angles_rates # (position, d_model)
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# apply sin to even indices in the array; 2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# apply cos to odd indices in the array; 2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...] # (1, position, d_model)
return tf.cast(pos_encoding, dtype=tf.float32)
2. Attention在Seq2Seq中的应用
在RNN组成的Seq2Seq模型中,假设序列长度为m:
- Encoder部分:对于每个时间步输入的$\boldsymbol{x}_i$,都会产生一个状态向量$\boldsymbol{h}_i$。一开始,该状态向量被初始化为$\boldsymbol{h}_0=\boldsymbol{0}$。在下一个时间步,通过某种运算,利用前一个时间步产生的\(\boldsymbol{h}_{t-1}\)与当前时间步的输入$\boldsymbol{x}_t$生成新的状态向量$\boldsymbol{h}_t$。重复上述步骤直至m个序列全部输入完成,得到一共m个状态向量$\boldsymbol{h}_1\sim \boldsymbol{h}_m$
得到$\boldsymbol{h}_t$的计算方式为:
\(\boldsymbol{h}_t = \boldsymbol{v}^T\cdot\rm{tanh}\left(W \cdot \left[\begin{array}{c} \boldsymbol{h}_{t-1}\\ \boldsymbol{x}_t \end{array}\right] + \boldsymbol{b}\right), where\:\boldsymbol{v}^T\:and\:W\:are \:trainable\:parameters\) - Decoder部分:对每个时间步有状态向量$\boldsymbol{s}_t$,在Encoder结束后,它被初始化为$\boldsymbol{s_0}=\boldsymbol{h}_m$。然后,在每个时间步$t$,使用align函数用$\boldsymbol{s}_t$与$\boldsymbol{h}_1\sim\boldsymbol{h}_m$分别计算得到一组对齐权重$\alpha_1\sim\alpha_m$(因为$\boldsymbol{h}_0=\boldsymbol{0}$,所以无需与其计算权重)。用计算得到的权重$\boldsymbol{h}_1\sim \boldsymbol{h}_m$加权,得到的加权平均向量即为context vector $\boldsymbol{c}_t$。接着,利用Decoder端的输入\(x^{\prime}_{t+1}\)、$\boldsymbol{c}_t$、$\boldsymbol{s}_t$更新\(\boldsymbol{s}_{t+1}\),……。重复上述步骤直至Decoder端没有输入为止(或Decoder输出结果为EOS)。
计算公式为:
\(\tilde{\alpha}_i=\boldsymbol{v}^T\cdot\rm{tanh}\left(W\cdot\left[ \begin{array}{c} \boldsymbol{h}_{i}\\ \boldsymbol{s}_t \end{array}\right]\right), for\:i\:=\:1\:to\:m\)
另外一种目前常用的计算权重的方法为(其中$W_K$和$W_Q$为可学习的参数):
\(\boldsymbol{k}_i=W_K\cdot\boldsymbol{h}_i, for\:i\:=\:1\:to\:m^\prime\\ \boldsymbol{q}_t=W_Q\cdot\boldsymbol{s}_t\\\ \tilde{\alpha}_i=\boldsymbol{k}^T_i\boldsymbol{q}_t, for\:i\:=\:1\:to\:m^\prime\)
归一化权重:
\([\alpha_1,\cdots,\alpha_m]=\rm{Softmax}([\tilde{\alpha}_1,\cdots,\tilde{\alpha}_m])\)
得到context vector:
\(\boldsymbol{c}_i=\sum^{m}_{k=1}\alpha_k\cdot\boldsymbol{h}_k\)
结合下一时刻输入,更新状态向量:
\(\boldsymbol{s}_{t+1}=\rm{tanh}\left(W^{\prime}\cdot\left[ \begin{array}{c} \boldsymbol{x}^\prime_{t+1}\\ \boldsymbol{s}_t\\ \boldsymbol{c}_t \end{array}\right] + \boldsymbol{b}\right)\)
在Transformer中,与上述过程类似,但要计算三组参数:Query:\(\boldsymbol{q}_{:j}=W_Q\boldsymbol{s}_j\),Key:\(\boldsymbol{k}_{:i}=W_K\boldsymbol{h}_i\),Value:\(\boldsymbol{v}_{:i}=W_V\boldsymbol{h}_i\),其中$i\in{1,\cdots,m}, j\in{1,\cdots,m^\prime}$。三组参数中Query是在Decoder端,用来匹配其它项;Key和Value在Encoder端,其中Key用于和Query匹配,Value则用于被加权平均。将\(\boldsymbol{k}_{:i}\)拼成矩阵$K$,\(\boldsymbol{v}_{:i}\)拼成矩阵$V$,\(\boldsymbol{q}_{:j}\)拼成矩阵$Q$。权重的计算公式为:
\(\boldsymbol{\alpha}_j=\rm{Softmax}(K^T\boldsymbol{q}_j)\in\mathbb{R}^m \tag{2}\)
在此基础上计算context vector:
\(\boldsymbol{c}_j=\alpha_{1j}\boldsymbol{v}_{:1}+\cdots+\alpha_{mj}\boldsymbol{v}_{:m}=V\cdot\rm{Softmax(K^T\boldsymbol{q}_{:j})}, for\:i\:=\:1\:to\:m^\prime \tag{3}\)
这里关于attention权重的计算,additive attention和dot product attention理论复杂度差不多,但dot product attention在实际中可以利用高度优化的矩阵乘法代码且更加节省空间,所以会更快。当向量的维度比较小时,两种attention机制表现差不多,但当向量维度变大时,additive attention优于dot product attention。作者认为是对于大的向量维度,点积值变得很大,从而使得softmax函数工作在饱和区(梯度很小)。如果方差太小,那么输出将会过于平坦,以致于无法有效地优化。如果方差太大,softmax将在初始化时饱和,从而使得学习变得困难。例如,假如Q、K均值为0,方差为1,则它们矩阵乘的结果将有均值为0,方差为$d_k$。为了解决这个问题,作者将dot product的结果乘上系数$\frac{1}{\sqrt{d_k}}$进行缩放,使得结果具有与$d_k$无关的一致的方差。最终attention公式如下:
\(C=\rm{Attention}(Q,K,V)=\rm{Softmax}(\frac{QK^T}{\sqrt{d_k}})V \tag{4}\)
论文中$h=8$为head数,$d_k=d_v=d_{model}/h=64$为key,value,query的维度。通过每个head内的降维操作,经过8个head后的结果拼接后可以获得和使用原始全部维度的single-head相似的计算开销。将Self-attention + Dense作为Encoder的一个block,由于输出与输入维度相同,所以可以堆叠多个block,论文中block数为6。官方代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def scaled_dot_product_attention(q, k, v, mask):
"""Calculate the attention weights.
q, k, v must have matching leading dimensions.
k, v must have matching penultimate dimension, i.e.: seq_len_k = seq_len_v.
The mask has different shapes depending on its type(padding or look ahead)
but it must be broadcastable for addition.
Args:
q: query shape == (..., seq_len_q, depth)
k: key shape == (..., seq_len_k, depth)
v: value shape == (..., seq_len_v, depth_v)
mask: Float tensor with shape broadcastable
to (..., seq_len_q, seq_len_k). Defaults to None.
Returns:
output, attention_weights
"""
matmul_qk = tf.matmul(q, k, transpose_b=True) # (..., seq_len_q, seq_len_k)
# scale matmul_qk
dk = tf.cast(tf.shape(k)[-1], tf.float32)
scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)
# add the mask to the scaled tensor.
# positions need to be masked out have value of 1.0
if mask is not None:
# mask multiplied with -1e9 (close to negative infinity). This is done because
# the mask is summed with the scaled matrix multiplication of Q and K and is
# applied immediately before a softmax. The goal is to zero out these cells,
# and large negative inputs to softmax are near zero in the output
scaled_attention_logits += (mask * -1e9)
# softmax is normalized on the last axis (seq_len_k) so that the scores
# add up to 1.
attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1) # (..., seq_len_q, seq_len_k)
output = tf.matmul(attention_weights, v) # (..., seq_len_q, depth_v)
return output, attention_weights
3. Self-attention在Transformer中的应用
Self-attention与上述attention的原理完全一致,区别是self-attention层只有一个输入序列$\boldsymbol{x}_i\in\mathbb{R}^m$,而attention层则需要两个(一个是原始序列,一个是目标序列)。该层拥有三组参数:Query:\(\boldsymbol{q}_{:j}=W_Q\boldsymbol{x}_i\),Key:\(\boldsymbol{k}_{:i}=W_K\boldsymbol{x}_i\),Value:\(\boldsymbol{v}_{:i}=W_V\boldsymbol{x}_i\)。Self-attention的输出为$m$个context vector向量,由于self-attention层与RNN有着同样的输入及输出,因此可以用self-attention来完全代替RNN。
4. Multi-Head Self-attention(Encoder)
Multi-head self-attention就是使用多个上文中的single-head self-attention,它们共享一个输入(一个序列),各自有着独立的参数并输出各自计算得到的context vector,最后将各head的输出堆叠即为multi-head self-attention层的输出。Multi-head self-attention层的每路输出(若输入序列长度为m,head数为d,则共有m路输出,每路为d个context vector的堆叠)会各自经过一个Dense层,再经过ReLU等激活函数产生新的输出\(\boldsymbol{u}_1,\boldsymbol{u}_2,\cdots,\boldsymbol{u}_m\),其中每路向量\(\boldsymbol{u}_{:i}\)都包含了序列中的所有信息。这里每路的Dense层共享参数,这是合理的,因为模型对每路的处理流程都是一样的。
5. Multi-Head Attention(Decoder)
与Multi-head self-attention类似,Multi-head attention原理也是如此,使用多个attention层,它们共享相同的输入(两个不同的序列),但各自有着独立的参数并输出各自计算得到的context vector,最后将各head的输出堆叠即为multi-head attention层的输出。
Decoder也由多个block组成,每个block由三层组成,第一层是Multi-head self-attention层,输入是$\boldsymbol{x}^\prime_1,\boldsymbol{x}^\prime_2,\cdots,\boldsymbol{x}^\prime_{m^\prime}$,输出为$\boldsymbol{c}^\prime_1,\boldsymbol{c}^\prime_2,\cdots,\boldsymbol{c}_{m^\prime}$。第二层是Multi-head attention层,该层输入序列为两个,一个为Encoder部分的最终输出,另一个为第一层网络生成的序列\(\boldsymbol{c}^\prime_1,\boldsymbol{c}^\prime_2,\cdots,\boldsymbol{c}_{m^\prime}\)。该层的输出为\(\boldsymbol{z}^\prime_1,\boldsymbol{z}^\prime_2,\cdots,\boldsymbol{z}_{m^\prime}\),是与输入同维度的向量。将第二层的各路输出经过一个Dense层(共享参数),再经过ReLU等激活函数产生新的输出\(\boldsymbol{s}^\prime_1,\boldsymbol{s}^\prime_2,\cdots,\boldsymbol{s}_{m^\prime}\),作为该block的最终输出。
6. Encoder+Decoder
通过将Encoder、Decoder结合起来,便组成了完整的Transformer模型:
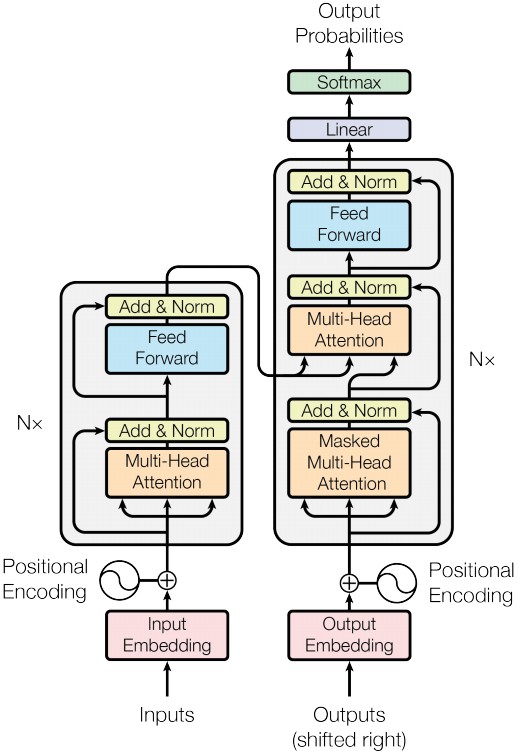
由于输出与输入维度相同,可以借鉴resNet的residual connection思想。具体做法是对于Encoder和Decoder每个block内部的子层(Encoder为两层,Decoder为三层),都使用skip connection将输入加到输出上去,然后再通过一个Layer Normalization层(即论文中的Add & Norm)。令$\rm{Sublayer}(x)$为每个子层的输出。那么,使用Add & Norm后每个子层的输出就变为:$\rm{LayerNorm}(x+\rm{Sublayer}(x))$。
为了避免模型注意到后续的位置信息,作者修改了Decoder中self-attention子层。这一masking结合一个事实:输出embedding会偏移一个位置。保证了对于位置$i$的预测仅依赖于已知的,$i$之前位置的输出。