为什么需要Normalization
深度学习训练中有一些常见的问题如梯度爆炸/消失,这一现象往往随着网络深度的增加而愈发凸显。为了解决这一问题,一个直接的想法就是:如果对每一层的输出数值范围都进行标准化,是否可以从某种程度上减轻这一现象呢?基于这个想法,Sergey Ioffe and Christian Szegedy于2015年提出了Batch Normalization,该方法使得深度神经网络训练的稳定性及训练效果都有了明显的提升。
目前主流的看法认为Batch Normalization(以下简称BN)可以解决神经网络中内部协变量偏移(internal covariate shift,即每层参数初始化及输入分布的改变会影响网络的学习率)的问题。但也有人认为BN并没有减轻“内部协变量偏移”,而是平滑了目标函数,从而提高了模型的性能。另外有文章认为BN实现了长度方向的解耦(length-direction decoupling),从而加入了神经网络的训练。使用BN作为模型的第一层可以使得模型不再需要feature scaling(使得模型对每个feature的sensitivity都相同)。
Internal covariate shift:神经网络每一层的输入都对应一个分布,该分布在训练期间受到参数初始化的随机性及输入数据的随机性的影响。这些随机性来源对训练期间网络内部层输入分布的影响被描述为内部协变量偏移。
BN也有缺点,在深度神经网络的初始化阶段,BN会引起严重的梯度爆炸,这一副作用只能通过残差网络中的跳连(skip connection)来解决。
Batch Normalization
BN最初被提出用于减轻内部协变量偏移,在网络的训练阶段,由于前面层参数的改变,当前层的输入分布也会随机改变,从而使得当前层需要不断调整自身参数以适应新的输入分布。这一问题对于深层的网络层更为严重,因为较浅层网络的微小改变会在网络的传播中被放大,最终在深层网络中产生显著的偏移。BN就是被设计用来减少这些不希望出现的偏移,从而加速训练并产生更可靠的模型。
除了减少内部协变量偏移,BN还带来了如下好处:网络可以使用更高的学习率训练而不用太考虑梯度爆炸/消失,虽然增加BN产生了额外的开销,但总的来说训练还是会变得更快。此外,BN某种程度上类似于对网络施加了正则,从而改善了模型的泛化能力,一定程度上减少了对dropout的依赖。BN还使得网络对参数初始化机制以及学习率更加鲁棒。
BN最好是使用全部训练数据的信息(均值、方差),但由于物理资源及数据规模的限制,一种更合理的方法是在训练过程中对mini-batch进行normalization(batch size要足够大以保证均值、方差估计的准确性)。记一个mini-batch为B,其对应m个训练样本。B的均值与方差即为:
\(\mu_B=\frac{1}{m}\sum_{i=1}^{m}x_i \\
\sigma_B^2=\frac{1}{m}\sum_{i=1}^{m}(x_i-\mu_B)^2 \tag{1}\)
对于输入维度为d的网络层,输入$x=(x^{(1)},\cdots,x^{(d)})$,输入的每个维度均被单独标准化:
\(\hat{x}_i^{(k)} = \frac{x_i^{(k)} - \mu_B^{(k)}}{\sqrt{\sigma_B^{(k)^2} + \epsilon}},\quad where\; k\in[1, d], \quad i\in[1, m] \tag{2}\)
上式中$\epsilon$是一个很小的非零值,用于避免除零错误。经过上步处理后的$\hat{x}^{(k)}$均值为0方差为1(不考虑$\epsilon$)。为了重建网络的表达能力,再对输入进行进一步变换:
\(y_i^{(k)}=\gamma^{(k)}\hat{x}^{(k)}+\beta^{(k)} \tag{3}\)
其中参数$\gamma^{(k)}$和$\beta^{(k)}$为可训练的参数,在优化过程中进行学习。对于每一层内部来说,输出一直为正态分布,由模型来学习真正适合下一层的输出数值范围。
BN操作是可微分的,直接使用链式法则求导即可。训练阶段,BN层参数靠mini-batch来保证有效的训练,但在推理阶段,将使用训练期间得到的统计数据来对输入进行标准化操作,即用计算得到的均值和方差期望来代替训练时所用数据:
\(E[x^{(k)}]=E_B[\mu_B^{(k)}], \quad Var[x^{(k)}]=\frac{m}{m-1}E_B[\sigma_B^{(k)^2}] \\
y^{(k)}=\frac{\gamma^{(k)}}{\sqrt{Var[x^{(k)}]+\epsilon}}x^{(k)}+(\beta^{(k)}-\frac{\gamma^{(k)}E[x^{(k)}]}{\sqrt{Var[x^{(k)}]+\epsilon}}) \tag{4}\)
以一维向量的样本为例,假设输入样本$x$的维度为$(1, d)$,则BN层的参数为$4\times d$个。若样本为图片,即输入样本$x$的维度为$(H, W, C)$,则BN层的参数为$4\times C$个(即对每个channel求一组$\mu,\sigma,\gamma,\beta$)。以求均值$\mu$为例,具体做法是将该batch内,所有N个样本的该channel对应的$H\times W$矩阵中,包含的所有元素求和取平均(除以$N\times H\times W$),最终得到$C$个标量值,对应$C$个channel的均值。完整公式如下:
\(\mu_c=\frac{1}{NHW}\sum_{i=1}^{N}\sum_{j=1}^{H}\sum_{k=1}^{W}x_{icjk} \\
\sigma_c^{2}=\frac{1}{NHW}\sum_{i=1}^{N}\sum_{j=1}^{H}\sum_{k=1}^{W}(x_{icjk}-\mu_c)^2 \\
\hat{x}=\frac{x-\mu_c}{\sqrt{\sigma_c^2+\epsilon}} \tag{5}\)
Layer Normalization
BN虽然好用,但是对于RNN这种recursive model,其每个时间步都具有不同的输入分布特性,此时BN将不起作用。为解决这一问题,Hinton团队于2016年提出Layer Normalization。Layer Normalization(后简称LN)与BN的区别是执行标准化操作的维度不同:BN是在batch的维度进行标准化(每个feature都有自己独立的均值、方差),LN是在feature的维度进行标准化(即每个样本都有自己独立的均值、方差),由于LN是对每个样本求均值和方差的,所以LN层只有两类参数:$\gamma$和$\beta$。
计算LN时,若输入为图片,即输入样本$x$的维度为$(H, W, C)$。以求均值$\mu$为例,具体做法是:将每个样本(对应一个$H\times W\times C$的三维矩阵)中的所有元素求和取平均,作为该样本的均值$\mu$。完整公式如下:
\(\mu_n=\frac{1}{CHW}\sum_{i=1}^{C}\sum_{j=1}^{H}\sum_{k=1}^{W}x_{nijk} \\
\sigma_n^{2}=\frac{1}{CHW}\sum_{i=1}^{C}\sum_{j=1}^{H}\sum_{k=1}^{W}(x_{nijk}-\mu_c)^2 \\
\hat{x}=\frac{x-\mu_n}{\sqrt{\sigma_n^2+\epsilon}} \tag{6}\)
Weight Normalization
BN是对网络层的输出进行标准化,那么为什么不直接标准化层的权值呢?Weight Normalization(2016年提出,下简称WN)。为了加速优化过程的收敛,WN将权值重新参数化为$\boldsymbol{w}=\frac{g}{\lVert\boldsymbol{v}\rVert}\boldsymbol{v}$,其中$v$是一个k维的向量,$g$是一个标量,$\lVert\boldsymbol{v}\rVert$是$\boldsymbol{v}$的欧式范数。这一操作使得权值向量$\boldsymbol{w}$的欧式范数值固定为g,从而使得神经元的activation范围近似独立于$\boldsymbol{v}$。WN可以看做是代价更低,具有更少噪声的BN的近似。此外,WN的确定性以及独立于mini-batch输入的特性使得WN也可以用于RNN,也可以用于强化学习等对噪声敏感的场景。
作者将mean-only batch normalization和weight normalization结合起来,即像BN一样减去mini-batch的均值,但不除以mini-batch的标准差,在训练期间维护一个mini-batch均值的移动平均以用于测试阶段代替均值。同时,使用WN来代替除以方差的操作。Mean-only batch normalization有着使反向传播的梯度居中的效果,而且这一操作也比BN有着更少的开销以及更少的噪声。这背后的原因是:依据大数定理,neuron activation的均值以及反向传播梯度的均值是近似正态分布的,从而其产生的噪声更加gentle。
Instance Normalization
Instance Normalization(2017年提出,下简称LN)是在BN、LN的基础上更细粒度的改进。IN相当于BN$\cap$LN但又有不同。IN与LN的不同之处在于:IN在每个训练样本的channel层面上进行标准化,而不是像LN那样在整个样本的层面上进行标准化。IN与BN的不同之处在于:IN层在推理阶段也会使用(因为mini-batch的无依赖性)。IN最早被计用于风格迁移中,因为图像风格化中,生成图片的结果主要依赖于某个独立的图片实例,所以不适合用BN来标准化,但可以针对HW层面做标准化以保持每个图像示例之间的相互独立。IN的参数维度将是$C\times N$。完整公式如下:
\(\mu_{nc}=\frac{1}{HW}\sum_{j=1}^{H}\sum_{k=1}^{W}x_{ncjk} \\
\sigma_{nc}^{2}=\frac{1}{HW}\sum_{j=1}^{H}\sum_{k=1}^{W}(x_{ncjk}-\mu_{nc})^2 \\
\hat{x}=\frac{x-\mu_{nc}}{\sqrt{\sigma_{nc}^2+\epsilon}} \tag{7}\)
Group Normalization
BN性能的保证有个前提条件是batch size要足够大,以保证统计特性估计的准确性。对于训练大的模型并迁移特征,以及包括目标检测、语义分割、视频等受显存限制而要求较小数据batch的计算机视觉领域,BN的使用受到了限制。此时Group Normalization(2018年提出,后简称GN)提供了一种在小batch size下使用Normalization的方法。GN将channel分割为多个group,则每个group有C/G(即为$c$)个通道,在每个group内分别计算均值和方差。GN的计算独立于batch size,且其准确性在较大的batch size选择范围内都比较稳定。GN是介于IN与LN之间的一种标准化方法。如果group数为1,则GN变为LN,如果group数等于channel数C,则GN变为IN。
假设通道数为G,则完整计算公式如下:
\(\mu_{ng}=\frac{1}{\frac{C}{G}HW}\sum_{i=1}^{C/G}\sum_{j=1}^{H}\sum_{k=1}^{W}x_{icjk} \\
\sigma_{ng}^{2}=\frac{1}{\frac{C}{G}HW}\sum_{i=1}^{C/G}\sum_{j=1}^{H}\sum_{k=1}^{W}(x_{icjk}-\mu_{ng})^2 \\
\hat{x}=\frac{x-\mu_{ng}}{\sqrt{\sigma_{ng}^2+\epsilon}} \tag{8}\)
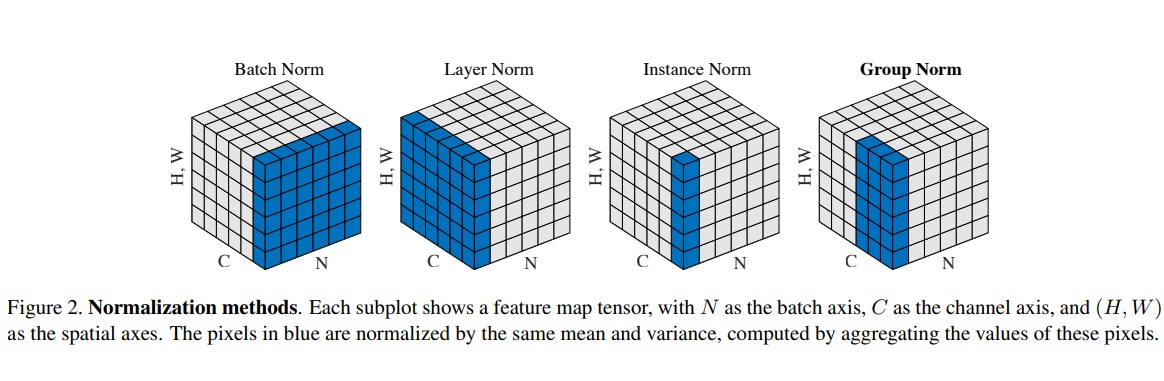
值得一提的是,作者以cubic的形式,形象地给出了BN、LN、IN、GN之间的对比关系:
Batch-Instance Normalization
使用IN的问题是:IN完全抹去了图片的风格信息(每个样本的channel单独normalize)。这对于风格迁移是优点,但对于对比度很重要的场景(如天气分类中,天空的明亮度很重要)这一特性又变成了缺点。Batch-instance normalization(2018年提出,下简称BIN)试图通过让模型学习每个通道需要多少风格信息,来解决上述问题。BIN可以看做是BN与IN的一个插值:
\(y = (\rho\cdot\hat{x}^{(B)}+(1-\rho)\cdot\hat{x}^{(I)})\cdot\gamma + \beta \tag{9}\)
上式中,参数$\rho$是一个可学习的介于0~1之间的参数,用于让模型自适应地决定BN与IN的比例。那么,是否可以让模型在需要的时候切换使用不同的normalization方法呢?于是便有了Switchable normalization。
Switchable Normalization
Switchable Normalization(2018年提出,下简称SN)使用了BN、IN、LN三种不同normalization方法所对应的均值、方差的加权平均值(权值为可训练的参数)。作者的结果显示:SN在图像分类及目标检测任务上有超越BN的潜力。研究结果还显示:在网络较早的层中IN使用的更多,中间层更倾向于使用BN,靠后的层更常使用LN。此外,更小的batch size会使得模型更倾向于LN及IN。