强化学习之——DQN的变种

DQN的变种

Double DQN

Double DQN是于2015年发表的文章“Deep Reinforcement Learning with Double Q-learning”中提出的，目的是减少DQN中常见的“高估”（overestimation）问题。
DQN中目标Q值的计算公式为：
$Q_{target}(s,a)\leftarrow r+\gamma max_{a’\in A}Q(s’,a’)\tag{1}\label{eq1}$
Bellman更新公式$\eqref{eq1}$中max算子使用同一个Q值来同时做动作选择及动作评估，这使得它更容易选择高估的值，从而导致过于乐观的值估计。Double DQN的核心思想：将动作选择与评估解耦可以减小上述效应的影响。
作者证明了任何原因造成的估计误差都会引起上偏（up bias）。Thrun and Schwartz (1993)证明：如果动作值包含均匀分布在$[-\epsilon, \epsilon]$内的随机误差，则每个目标值被高估的误差上界是$\gamma \epsilon \frac{m-1}{m+1}$。Double DQN作者给出了相应的误差下确界，并证明了在造成经典DQN高估的同样条件下，Double DQN的误差下确界是0：

与经典DQN的区别是：使用online network来评估贪心策略（进行动作选择），使用目标网络来估计值（进行值估计）。所以，Double DQN的目标Q值计算公式变为：
$Q_{target}(s,a)\leftarrow r+\gamma Q(s’, argmax_{a}(s’,\theta_t),\theta_{t}^{-})\tag{2}$
上式中$\theta_{t}^{-}$是target网络的参数，$\theta_{t}$是当前online网络的参数。对应的TensorFlow代码实现为

import tensorflow as tf

def train_on_batch(self, states, actions, rewards, next_states, dones):
    actions = tf.cast(actions, dtype=tf.uint8)
    # using target network to calculate Q values
    next_Q_values = self.model_target(next_states)
    # using online network to select eager action 
    next_mask = tf.one_hot(np.argmax(self.model(next_states), axis=1), depth=2, dtype=tf.float32)  
    target_Q_values = (rewards + (1 - dones) * self.gamma * 
                        tf.reduce_sum(next_Q_values * next_mask, axis=1, keepdims=True))

    mask = tf.squeeze(tf.one_hot(actions, depth=2, dtype=tf.float32))
    with tf.GradientTape() as tape:
        Q_values_ = self.model(states)
        Q_values = tf.reduce_sum(Q_values_ * mask, axis=1, keepdims=True)
        loss = tf.reduce_mean(tf.keras.losses.MSE(target_Q_values, Q_values))
    gradients = tape.gradient(loss, self.model.trainable_variables)
    self.optimizer.apply_gradients(zip(gradients, self.model.trainable_variables))

Prioritized Double DQN

DQN算法可以从大的replay buffer中收益，训练时每次从中等概率随机选取一个batch的样本来进行训练。2016年的一篇文章PRIORITIZED EXPERIENCE REPLAY提出了prioritized experience replay，核心思想是强化学习agent可以从某些样本中以更快的速度学到更有价值的信息（相比于其它样本），即样本具有不同的“优先级”。如何量化样本优先级呢？一个合理的选择是temporal difference (TD) error，以更频繁的方式选择有着更高“优先级”的样本来进行训练。这样做也会带来一个问题，就是训练loss的多样性受到损失，这可以通过随机优先排序来消除，而随机优先排序又引入了新的偏差（bias），这一偏差可以用重要性采样来纠正。
TD error $\delta$表明了一个transition带来多大的“意外”，即这一新的transition与当前模型的预期（当前模型预测的Q值）有多大的差异。

随机采样法
贪心TD error $\delta$优先级方法（即选择有最大TD error的几个样本训练）有几个问题：（1）replay buffer可能很大，为了避免在整个大replay buffer上进行扫描，仅对于使用过的样本才进行TD error更新，这样做可能还是得具有低TD error的样本将在很长一段时间内不会被使用；（2）对于噪声很敏感（比如当奖励是随机的），这一噪声可能会被bootstrapping放大（类似的还有函数近似误差，容易造成overestimation）；（3）贪心优先级法仅关注经验集中很少一部分样本，误差缩减很慢（尤其是在使用函数近似时），这意味着初始具有高误差的样本会被频繁地使用，从而使得系统倾向于对这些样本过拟合。
为克服这个问题，采用随机采样法，该方法在纯粹的贪心优先级法及均匀随机采样之间进行了折衷。该方法保证了被采样的样本的概率与样本优先级的关系是单调的，同时保证了即使具有最低优先级的样本也有非零的被采样概率。具体地，第i个样本采样概率为：
$P(i)=\frac{p_i^\alpha}{\sum_kp_k^\alpha}\tag{3}\label{eq3}$
其中$p_i>0$是样本$i$的优先级。指数$\alpha$表明了多大程度上使用了优先级，$\alpha=0$时退化为均匀采样，$\alpha=1$时为完全按照优先级采样。
优先级$p_i$的选择有两种实现方式：
1. $p_i=|\delta|+\epsilon$，其中$\epsilon$是小的正常数来保证所有样本的采样概率都不为0。
  为了实现从分布$\eqref{eq3}$中高效地采样，线性时间复杂度O(N)无法满足需求。对于该实现方式，可以使用“sum-tree”的数据结构，支持对数线性的时间复杂度进行更新和采样。
2. $p_i=\frac{1}{\mathrm{rank}(i)}$，其中$\mathrm{rank}(i)$是replay buffer按照$|\delta|$排序（从高到低）后第$i$个样本的序号。
  对于基于排序的实现方式，可以用$k$（$k$=batch size）个分段线性函数来近似累积密度函数（cumulative density function, CDF）。使用时，采样$k$个段，再对每段内等概率采样一个样本——分层采样。
偏差退火
随机更新期望值的估计，依赖于与期望有着分布相同的更新。Prioritized replay由于改变了样本分布而引入了偏差，从而改变了其估计值的收敛结果（尽管策略及状态分布是固定的）。这一偏差可以通过使用重要性采样权值（importance-sampling weights，可能翻译为优先级采样权值更合适）来补偿：
$w_i=(\frac{1}{N}\cdot\frac{1}{P(i)})^\beta\tag{4}$
上式中，如果$\beta=1$代表对非均匀采样进行完全补偿，$\beta=1$代表完全不进行补偿。这些权值被用在Q-learning的更新时：用$w_i\delta_i$代替$\delta_i$。出于稳定性的考虑，需要对权值进行归一化：除以${\mathrm max}_iw_i$。
在典型的强化学习场景中，由于策略，状态分布及bootstrap得到的目标的不断变化，训练过程是高度非平稳的。因此，在接近训练结束时，更新的准确性（无偏）更为关键。作者假设小的偏差可以被忽略（在训练早期，不平稳性因素较多）。为了使策略变得更灵活，作者引入了参数退火：训练过程中，参数$\beta$从初始的$\beta_0$逐渐减小至1（完全补偿）。实际操作中为线性变化。参数$\beta$与$\alpha$共同起作用，应同时增/减二者以调节参数（同时增加意味着采用更强的优先级采样，也因此需要更多的偏差矫正）。
使用了Prioritized replay buffer的Double DQN算法如下图：

使用O(N)时间复杂度Prioritized replay buffer的Double DQN算法TensorFlow实现。
Dueling DQN

Dueling DQN出自2016年文章Dueling Network Architectures for Deep Reinforcement Learning。相比于DQN中直接预测Q值的方式，将Q值分解为状态值+（动作）优势值有助于算法更快的收敛。Dueling DQN不再直接预测$Q(s,a)$，而是分别预测状态值函数$V(s)$和优势函数$A(s,a)$，然后将二者组合来产生Q值：$Q^\pi(s,a)=V^\pi(s)+A^\pi(s,a)$。这一做法的原因是，很多时候我们并不关心每个候选动作的具体Q值是多少，更关心的是选择哪个动作能带来更大收益。
具体在网络结构方面，网络的最后一层全连接层修改为两层全连接层，这样做的目的是为了给值函数和优势函数提供单独的估计。最后，二者组合生成所需的Q值。Dueling DQN与传统DQN网络结构的对比如下图：

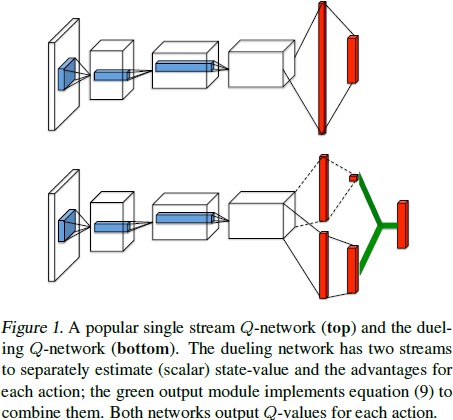
值得注意的是，虽然最终获得的是Q的估计值，但网络中作为状态值函数V以及优势值函数A的两部分网络所输出的值，不能被当作状态值V以及优势A的较好估计。
【P.S.】我个人觉得这里网络结构修改非常类似于神经网络中预测“残差”的思想，有助于训练过程的稳定。
Dueling DQN网络结构所表达的含义可以写为$Q(s,a;\alpha,\beta)=V(s;\theta,\beta)+A(s,a;\theta,\alpha)$。但是虽然网络的两部分输出被设计用来估计状态和优势函数，但对于网络来说一意图这是“无法识别的”，为了解决这个问题，作者强制优势函数估计器对于所选动作优势值为0。具体实现是从优势输出估计中减去优势值中的最大值：$Q(s,a;\alpha,\beta)=V(s;\theta,\beta)+(A(s,a;\theta,\alpha)-max_{a’\in|A|}(s,a’;\theta,\alpha))$。这样便能一定程度上保证状态值估计器部分提供值函数的估计，优势值估计器部分提供关于优势的估计。
另一种做法是减去均值：$Q(s,a;\alpha,\beta)=V(s;\theta,\beta)+(A(s,a;\theta,\alpha)-\frac{1}{|\mathcal{A}|}\sum_{a’}A(s,a’;\theta,\alpha))$。这样做一方面使得V和A失去了明确的含义，因为对二者都引入了一个偏移。另一方面，这样做增加了优化的稳定性：优势估计只需要适应该部分均值的改变而不是需要适应最大值（最优动作的优势），而均值自然比最值要稳定很多。减去均值有助于提高“识别度”的同时并不会改变优势值（包括Q值）的相对顺序，从而保证了基于Q值的贪心算法的有效性。
Dueling DQN基于TensorFlow的算法实现

Noisy DQN

该内容出自2018年文章NOISY NETWORKS FOR EXPLORATION，该技术的提出是为了解决exploration vs. exploiration中的探索问题。大多数关于探索的强化学习研究都是依赖于对策略的随机扰动，比如$\epsilon$-greedy或者使用熵正则。另外还有添加“instrinsic reward”等方法，这些方法都需要算法使用者自定义参数，而不是从与环境的交互中学习。直接探索策略空间的方法（如进化或黑箱算法）通常要求与环境多次长时间交互。作者的核心观点是：对于权值向量的一个简单改变，可以在多个时间步上引发一致，复杂，状态依赖的策略改变。不同于添加无关扰动的方法（如$\epsilon$-greedy），这里的扰动是从一个噪声分布中采样得到的。扰动的方差是一个可学习的参数，该参数可以被看做注入的噪声的能量。
噪声网络的权重与偏置都被参数化的噪声函数扰动，这些参数由梯度下降来更新。令$y=f_\theta(x)$代表由噪声参数$\theta$参数化的神经网络，将噪声参数$\theta$表示为$\theta\overset{\text{def}}{=}\mu+\varSigma\bigodot\varepsilon$，其中$\zeta\overset{\text{def}}{=}(\mu,\varSigma)$是一组可学习的参数向量，$\varepsilon$是一个具有不变统计特性的零均值噪声。
考虑一个神经网络线性层，该网络层具有$p$个输入及$q$个输出：$y=wx+b$，对应的噪声线性层定义为：
$y\overset{\text{def}}{=}(\mu^w+\sigma^w\bigodot\varepsilon^w)x+\mu^b+\sigma^b\bigodot\varepsilon^b\tag{5}$
其中$\mu^w+\sigma^w\bigodot\varepsilon^w$与$\mu^b+\sigma^b\bigodot\varepsilon^b$分别替换$w$和$b$。其中$\mu^w,\mu^b,\sigma^w,\sigma^b$是可学习的参数而$\varepsilon^w,\varepsilon^b$是随机噪声变量。
有两种线性噪声层的实现方式：
独立高斯噪声
添加到每个权重及偏置的噪声是相互独立的，其中随机矩阵$\varepsilon^w$（及其相应的$\varepsilon^b$）中每项$\varepsilon_{i,j}^w$（及其相应的$\varepsilon_{i,j}^b$）是从标准正态分布中选择。这意味着对每个噪声线性层，有$pq+q$个噪声变量。
因式分解高斯噪声
通过分解$\varepsilon_{i,j}^w$，可以使用$p$个标准正态分布变量$\varepsilon_i$作为输入噪声，$q$个标准正态分布变量$\varepsilon_i$作为输出噪声（所以总共$p+q$个高斯变量）。每个$\varepsilon_{i,j}^w$和$\varepsilon^b$可以被写作：
$\varepsilon_{i,j}^w=f(\varepsilon_i)f(\varepsilon_j)\ 和\ \varepsilon_j^b=f(\varepsilon_j)\tag{6}$
其中$f$是实值函数，作者使用的是$f(x)={\mathrm {sign}}\sqrt{|x|}$。对于噪声网络的损失函数$\overline{L}(\zeta)=\mathbb{E}[L(\theta)]$是噪声的期望，其梯度计算公式：
$\nabla\overline{L}(\zeta)=\nabla\mathbb{E}[L(\theta)]=\mathbb{E}[\nabla_{\mu,\varSigma}L(\mu+\varSigma\bigodot\varepsilon)]\tag{7}$
作者对上述梯度使用蒙特卡洛近似，每一步选取一个样本$\xi$进行优化：
$\nabla\overline{L}(\zeta)\approx\nabla_{\mu,\varSigma}L(\mu+\varSigma\bigodot\xi)\tag{8}$

Noisy DQN基于TensorFlow的算法实现

DQN variants

DQN的变种

Double DQN

Prioritized Double DQN

Dueling DQN

Noisy DQN

CATALOG

FEATURED TAGS